Conditional Gradient / Frank-Wolfe

Revisiting a projection-free method

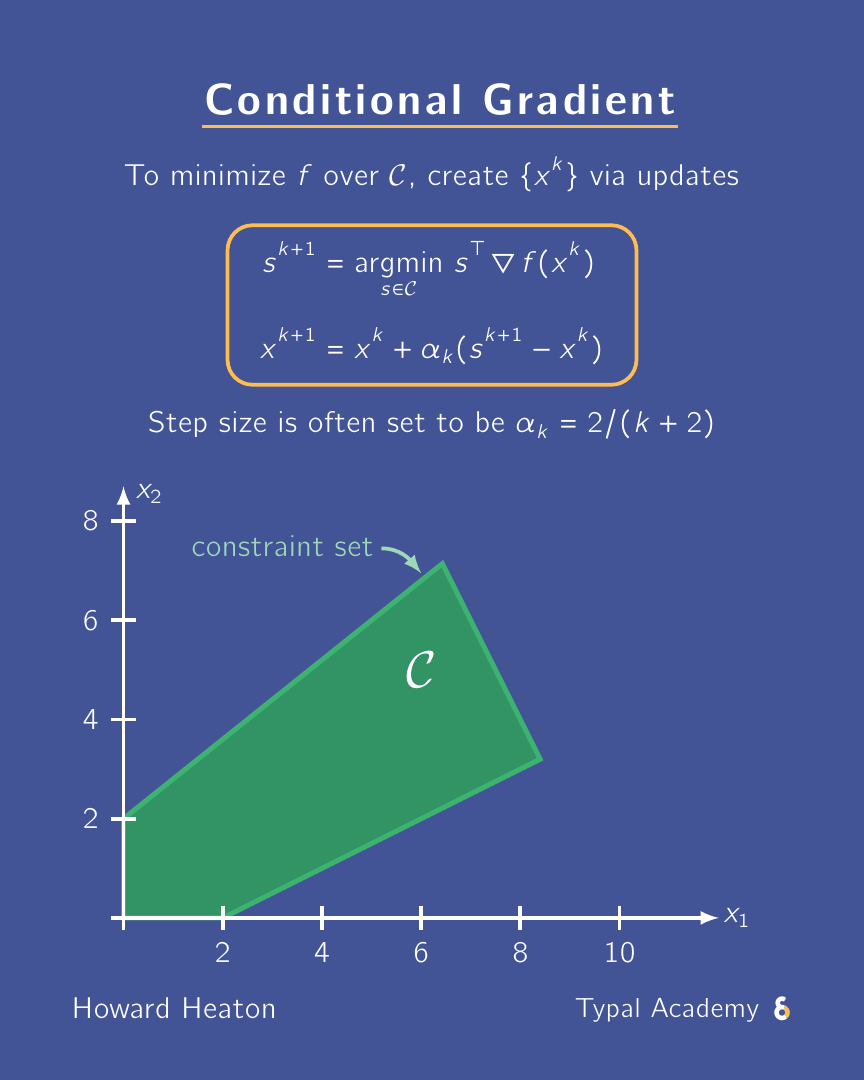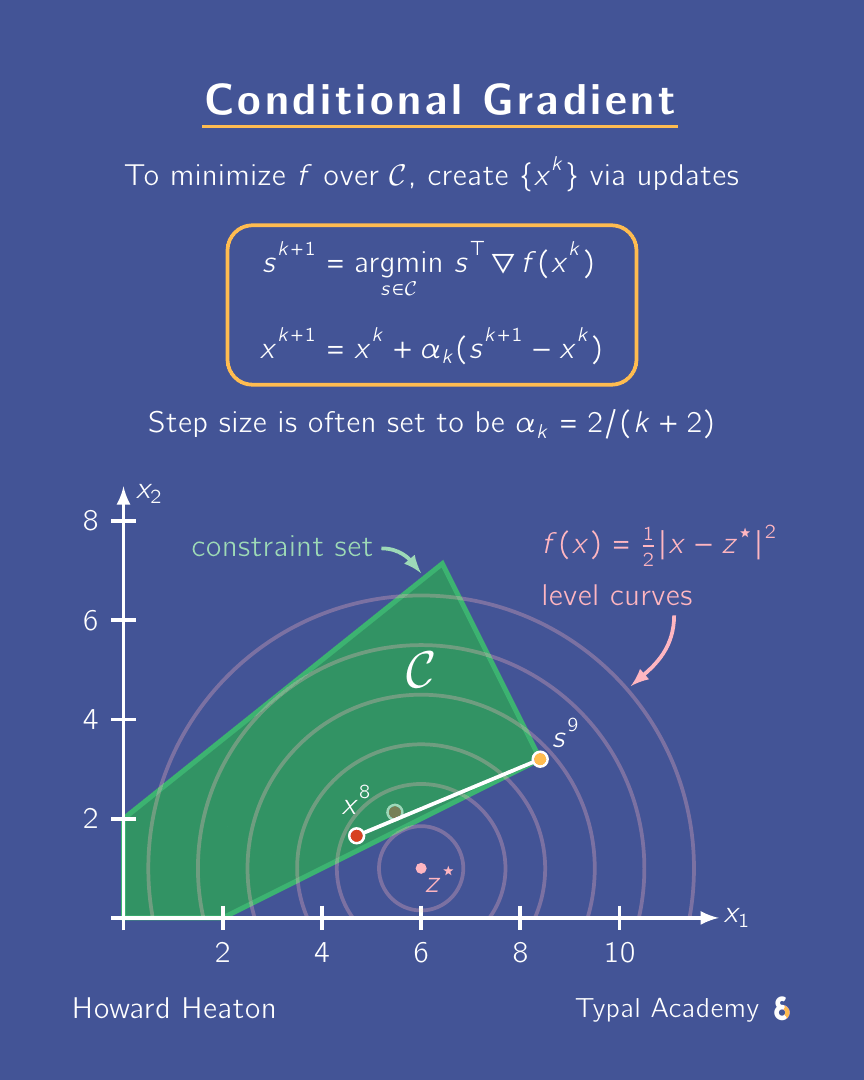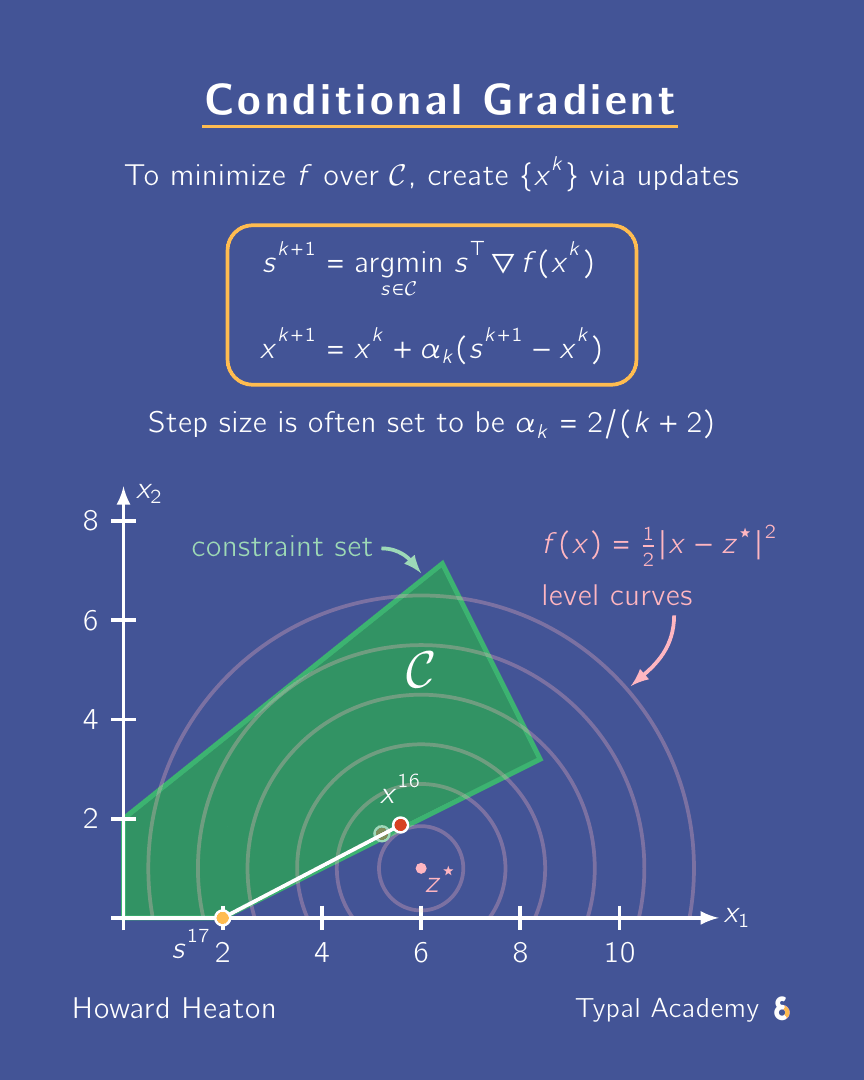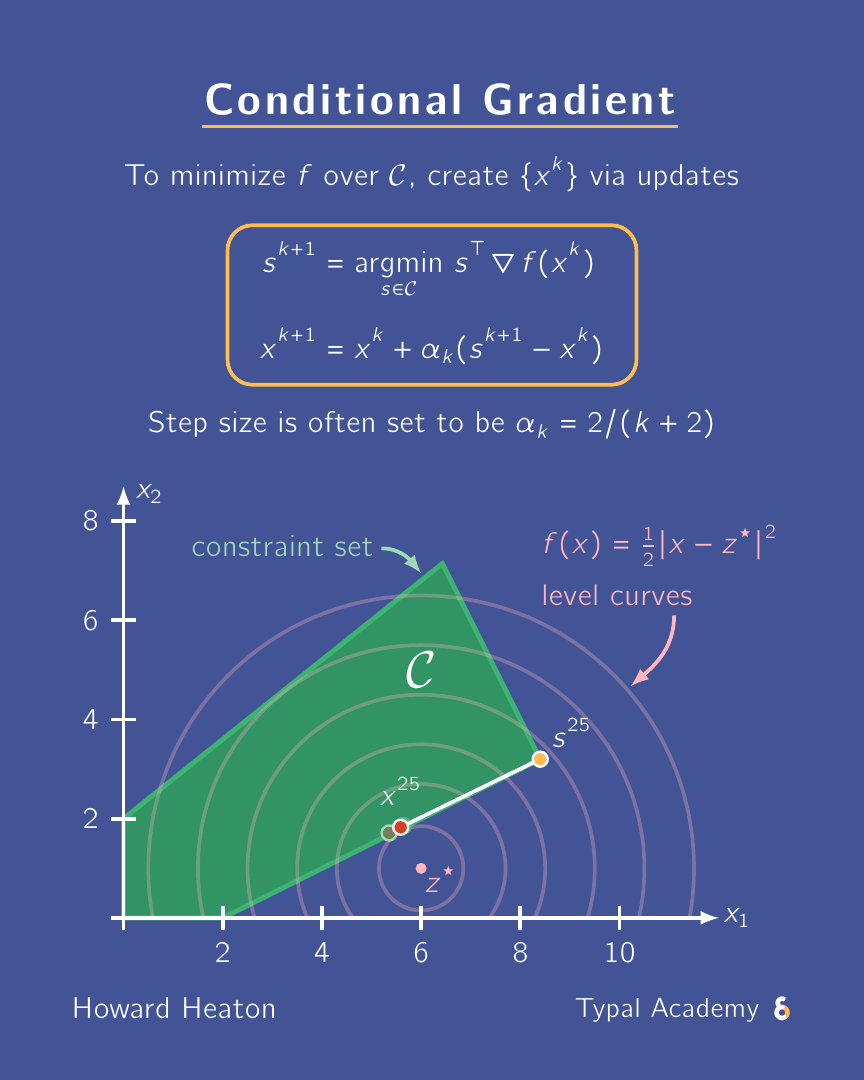
A need-to-know scheme for constrained optimization: conditional gradient a.k.a. Frank-Wolfe. Why? Scalable, projection-free, can exploit sparsity. ✅

In some settings, conditional gradient outperforms proximal-based methods (e.g. proximal gradient). This can occur since each update step uses linear subproblems rather than quadratic, which can significantly reduce computational costs. When the constraint is a convex hull of atomic sets, as is the case in many relaxation of NP-hard problems, conditional gradient updates are naturally "sparse" by using one atom per iteration.

𝗛𝗼𝘄 𝗶𝘁 𝘄𝗼𝗿𝗸𝘀:

1. Minimize dot product with gradient over constraint set.

2. Average result of Step 1 with current solution estimate.

Repeat until converge.

In some important applications, Step 1 admits a "nice" formula.

Often, the weight for averaging is chosen to be 2 / (k + 2) for the result of Step 1 and 1 - 2 / (k+2) for the current estimate, where k is the iteration index.

𝗞𝗲𝘆 𝗙𝗲𝗮𝘁𝘂𝗿𝗲𝘀:

- Simple

- Linear Subproblems (No Projections)

- Affine Invariance (Mitigates Ill-Conditioning)

- Convergence Guarantees

Conditional gradient has received renewed interest for its suitability in some high-dimensional problems.

The animation above shows an example for how it executes. Here is a link to a YouTube Short where I briefly overview it.

Cheers,

Howard

p.s. For more details, I highly recommend reading Martin Jaggi's paper Revisiting Frank-Wolfe: Projection-Free Sparse Convex Optimization. It's a great paper and was the main source for this post. Access it below (n.b. Conditional Gradient is also called “Frank-Wolfe”).