Douglas Rachford Splitting

Minimize a sum of nonsmooth functions

Two convex functions were added. A minimizer was
sought, but neither function was differentiable.
Luckily, we had Douglas-Rachford splitting. ✅

When dealing with nonsmooth functions,
popular algorithms like gradient descent may not be apt.
Instead, Douglas Rachford Splitting (DRS) can be ideal.
DRS can be particularly effective with
L1 norms, nuclear norms, and various hard constraints.

The applications where this problem can arise are many.
I actually wrote a paper on DRS with numerical examples
for basis pursuit, stable principal component pursuit,
earth mover's distances, and stable matrix completion.
It performed better than the benchmarked schemes.

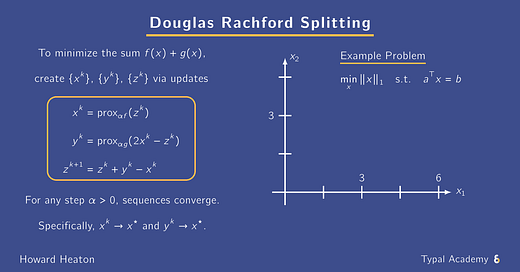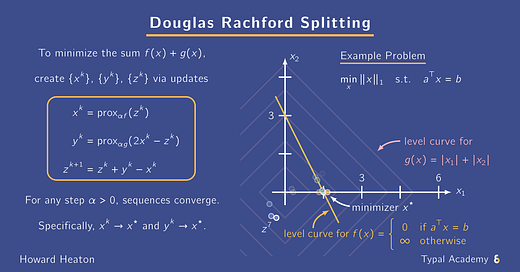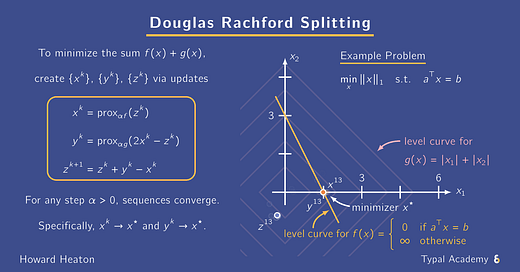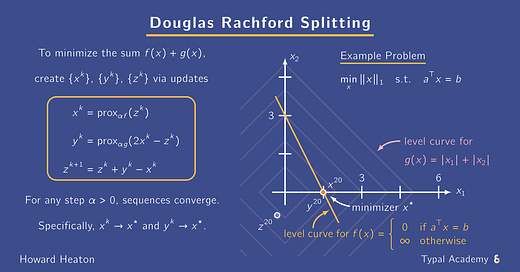
To visualize how it executes,
check out the animation below
with an L1 norm and linear constraint.

I also made a 4 minute YouTube video overviewing DRS:

Cheers,

Howard